I found a solution. The left side of the patch gives the correct answer but the right side doesn’t. It seems strange that I need to go through an additional step. But it works…
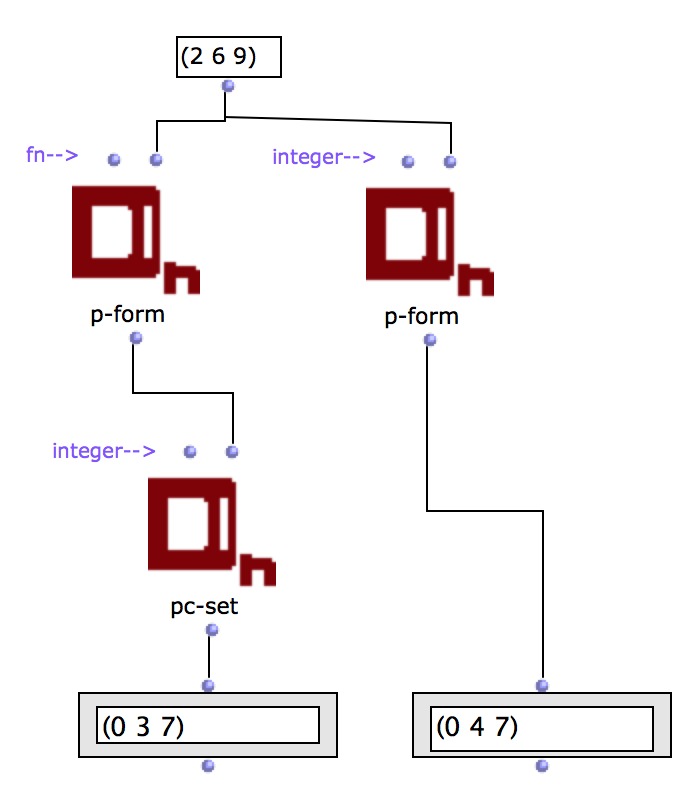

I found a solution. The left side of the patch gives the correct answer but the right side doesn’t. It seems strange that I need to go through an additional step. But it works…

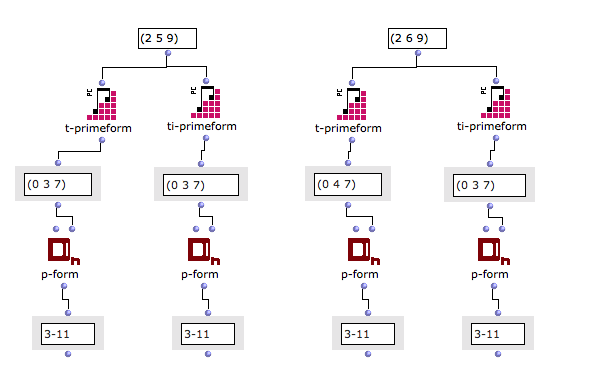
I am now convinced that there is a problem with p-form. See image. It works correctly for some sets but not others.
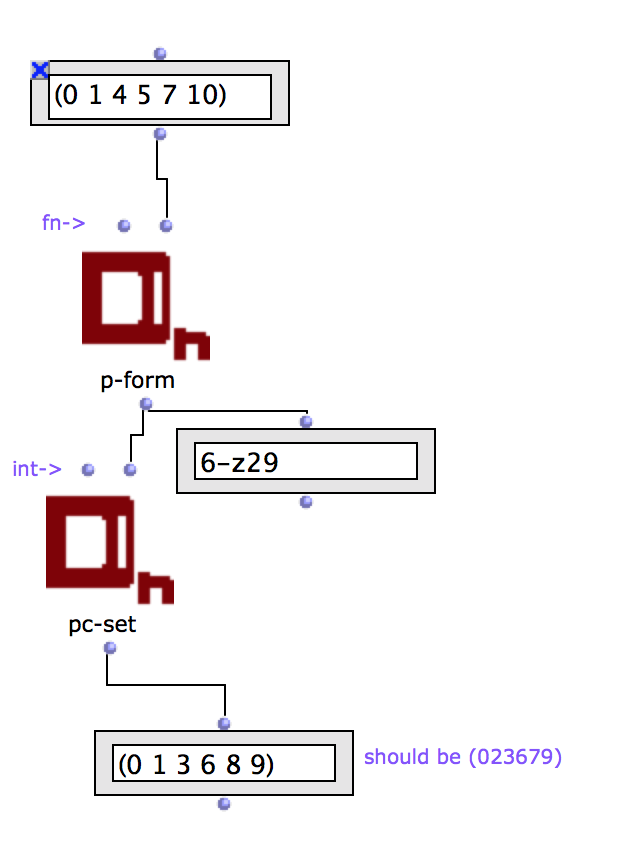
May be this could help !
Hello fiboribo,
Welcome to the forum. It interests me that we can exchange.
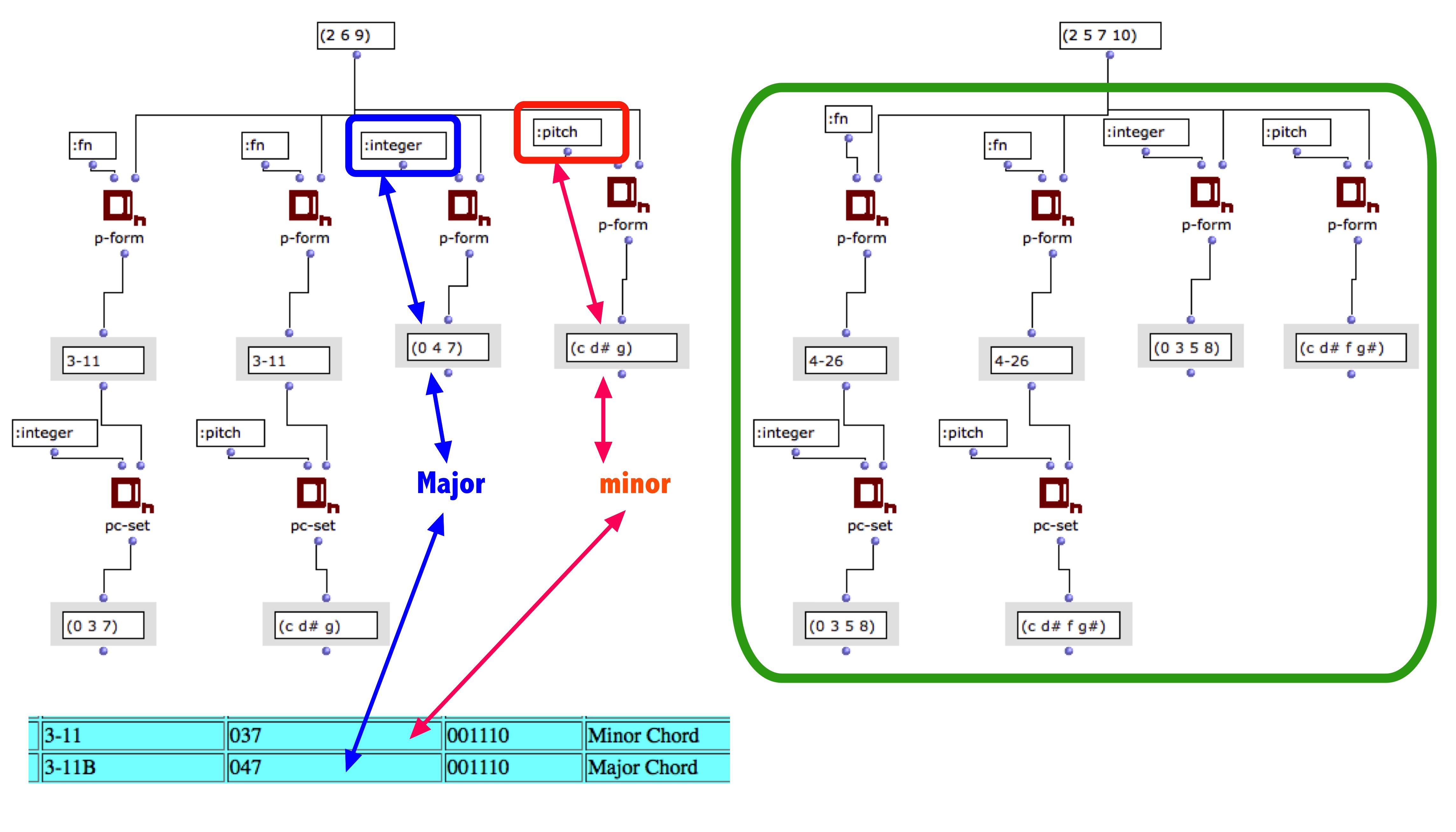
Otherwise, it’s actually surprising these two results. But this is perhaps due to the fact that Allen Forte is no difference in the pc-set 3-11 between the major chord and the minor chord. For him, this is the same set.
But I notice that according to the entry with P-form, and pitch between integer, integer displays all major and pitch, the minor.
Sorry for my bad english.
Didier
have a look at this http://solomonsmusic.net/pcsets.htm, especially, # 182 as you can see we got (0,1,3,6,8,9)
your set seems to be an exception !
Bonjour,
Dans la librairie OMPitchfield, il y a deux fonctions qui affichent la prime-form et dont une prend en compte la différence dans un accord parfait 3-11 entre majeur et mineur, contrairement à Dn-p-form. Ainsi, la fonction PC-ti-primeform est semblable à Dn-p-form tandis que PC-t-primeform affiche bien la différence entre accord parfait mineur et majeur.
Hello,
In the OM-Pitchfield library, there are two functions that display the prim-form and one takes the difference in triad chord 3-11 between major and minor, contrary to Dn-p-form. Thus, the PC-ti-PrimeForm function is similar to Dn-p-form while PC-t-primeform displays the difference between minor and major triad chord.
Didier
Thank you all. This is very helpful!
Federico
A tout patcheur !!!
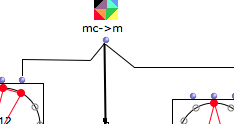
Je voudrais attirer votre attention sur les liens que crée OM par défaut : voir “par défaut” où un doute s’installe sur le “câblage” des cercles. Logiquement les deux cercles sont câble au “mc->m” mais on peut avoir un doute.
Ainsi, je vous invite à mettre des liens obliques : voir “oblique” ainsi aucun doute n’est permis !
cela peut paraître anodin, mais je poste ce commentaire puisque, quoiqu’il en soit, il fallait que je le fasse !
……………………………………………………………………………… jerome
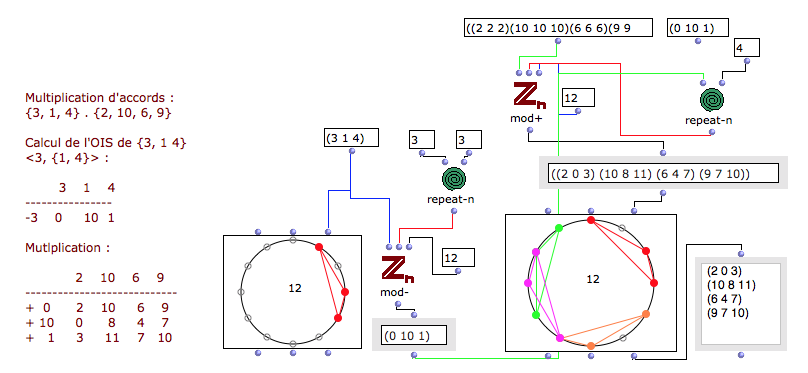
A propos de la multiplication d’accord…
sur la page 19 figure 3 de “QUELQUES PROPRIETES DE LA TECHNIQUE DE ´ BOULEZ
DE MULTIPLICATION DES BLOCS SONORES de Nicolas Weiss” (voir PJ)
on voit deux exemples des transposition de A sur B et le A X B
Si sur le second (avec A et B ayant chacun deux notes) tout est limpide on retrouve bien 4 notes, Sur le premier (avec A et B ayant chacun 3 notes) On voit que A X B donne bien B mais avec 7 notes en tout… Pourquoi ?
Merci d’avance
……………………………………………………………………… jerome

est-ce qu’en fait on obtiendrait 9 notes mais qu’il y aurais 2 unissons du au mod 12 ?
Bonjour Jérôme,
Effectivement, il y a 9 hauteurs (3*3 = 9) alors que dans le bloc sonore final il n’y a que 7 hauteurs. C’est dû aux deux notes communes La# et Ré#. Dans ce cas, Boulez ne retient qu’une seule instance d’une hauteur et il élimine les hauteurs en doublons (lire page 168 dans Relevé d’apprenti). Dans la copie d’écran qui reproduit le calcul à la main, j’ai entouré les hauteurs communes.
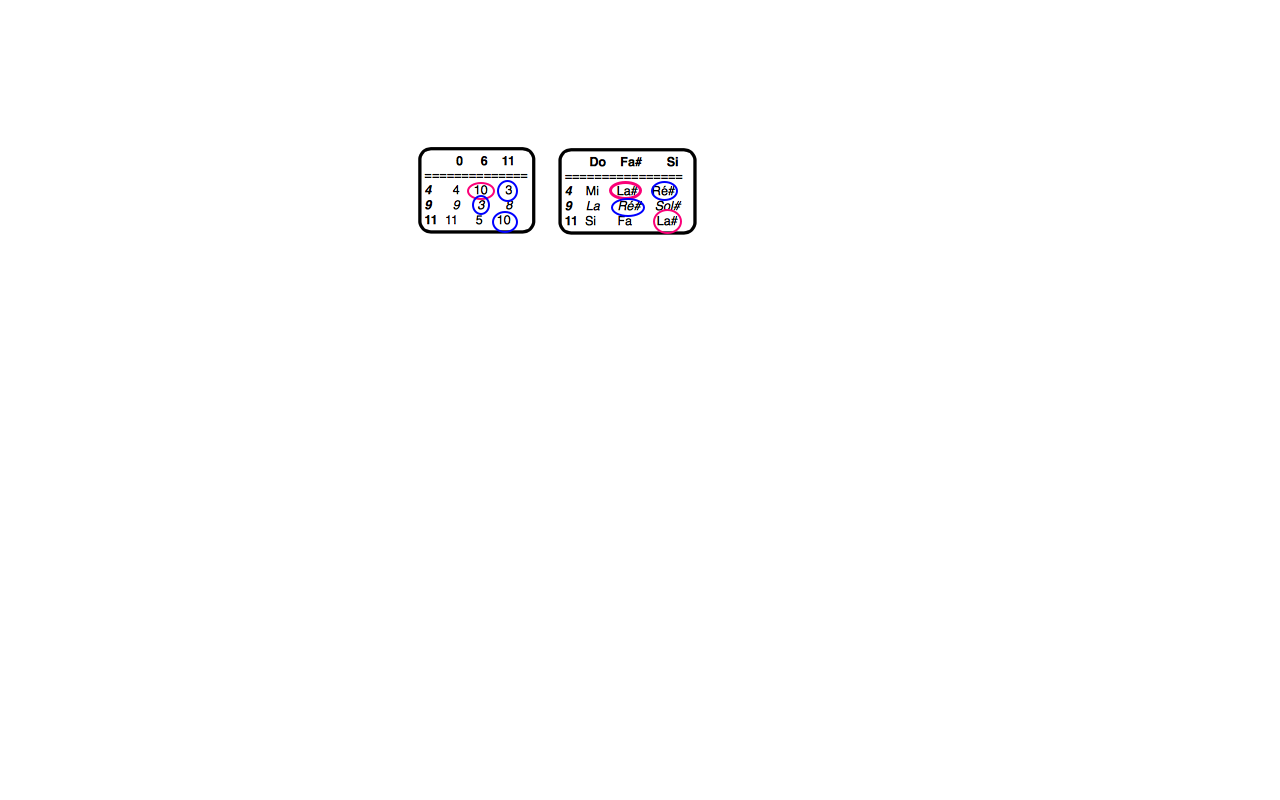
ok ! merci
Quand j’ai essayé de comprendre cette multiplication d’accords, j’ai pas mal galéré car j’effectuais mes calculs à partir des hauteurs et non pas en transférant la structure intervallique d’un des blocs sonores sur chacune des hauteurs du second bloc. D’où des résultats corrects en majeure partie mais pas totalement. Et c’était dû à une mauvaise lecture de ma part des explications de Boulez ou des exemples cités. Mais j’ai enfin compris mon erreur grâce à cette thèse mise en ligne sur le “ResearchWorks Archive” de la librairie digital de Washington : “Pitch-class set multiplication in Boule’s Le Marteau sans maître” (https://digital.lib.washington.edu/researchworks/handle/1773/11257). Je conseille vraiment la lecture de ce document qui s’appuie sur les termes, symboles et conventions de notation sur l’ouvrage de John Rahn “Basic Atonal Theory”.
Ca m’a l’air très intéressant, En lisant l’intro, je vois que la multiplication reste commutative, ce qui est logique mais qui me titillait un peu
Merci pour ce PDF,
Cheers~
……………………………………………………………………… jerome
J’ai quelques problèmes avec la méthode manuelle (l’OIS et l’analyse du “marteau sans maitre” qui en découle). je vais regarder dans la thèse ci-dessus pourvoir si cela m’éclaire.
Par contre, j’ai bien comprise la méthode computationelle !
Merci d’avance
……………………………………………………………………………… jerome

Bonjour Jérôme,
-3 0 10 1 l’OIS = 0, 10, 1
Dès lors, cette multiplication, que certains décrivent comme étant une opération complexe, est aisée. Elle consiste à reporter chacun des intervalles de l’ECH {3, 1, 4} sur chacune des hauteurs de l’ECH {2, 10, 6, 9}. Ces dernières hauteurs étant introduites dans le résultat de l’opération modulo 12 grâce à l’OIS et la transposition du do, soit 0 :
2 10 6 9 ----------------------------
Il suffit de reporter le résultat en enlevant les doublons 7 et 10 et on obtient le résultat de Pierre Boulez. J’ai fait un PDF avec des copies d’écran qui expliquent pas à pas ces opérations “manuellement” ou en simulant le calcul manuel avec les opérateurs d’OM et confirmées avec le résultat de Zn-transp-comb. Et je mets aussi en pièce jointe le fichier OM.
Ceci étant, la thèse de Stephen Heinemann est très intéressante à lire, elle donne beaucoup de clés de compréhension sur les diff:érentes opérations modulo 12.
Didier
PS : Désolé pour les calculs en “matrice”, la mise en page m’enlève les espaces. Résultat ce n’est pas très lisible. Dès lors, il faut se référer au PDF.
Cher Didier,
En effet, c’est pas très compliqué… Je crois que je me suis compliqué l’affaire tout seul !
Un grand merci pour cette explication limpide !
…………………………………………………………………………… jerome
Pour en finir avec ce topic,
voir PDF
Cheers~
…………………………………………………………………………………………………………… jerome
OIS-end.pdf (315 KB)
Bonjour Jérôme,
Désolé de ne pas avoir répondu plus tôt. Je t’ai fait un autre Pdf à partir d’un exemple sur la multiplication d’accords de P. Boulez de Catherine Losada. Elle montre bien avec des flèches la transposition des intervalles du premier accord sur chacune des notes du second accord. Et ça permet de voir que l’OIS établit bien la nature des transpositions des intervalles. En l’occurence dans les deux exemples T3 et T5. Et du coup, je me suis demandé si à partir de l’OIS on pouvait calculer les fonctions dédiées x->dx et Zn-structure et vice-versa avec les opérateurs arithmétiques d’OM, ainsi que leur calcul “à la main” sans ordinateur, pour comprendre le processus.
Bien à toi.
Didier
OISTranspo.pdf (1.69 MB)
Good morning from Athens
I’m a new member in the Set Theory and Open Music Group.
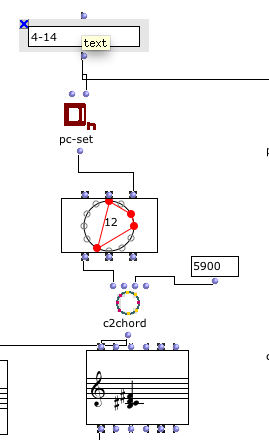
I’m trying to find a way to produce exactly the same order (6 4 11 3) —
in 4-14 ( ic-vector 111120----(0 2 3 7))in order to have it as 7 5 0 4 '(for melody purposes )
when I use z-related pc-sets or super sets (like 8-z15) for example , I want to have the same order
not in the prime form but as I did it in the first appearance (6 4 11 3) in 4-14 .
I’m doing it by hand , but I thing there is an easier way to do it.
( the following is a way not correct, because I have the prime form, a semitone below (due to the 5900 in c2chord)
but not in the order I want -----(6 4 11 3) = (7 5 0 4)= (6 2 11 1), (thats a transposition )
Can you help me or make a suggestion to have the order of the first choice , in supersets etc
Yours sincerely
Thanassis