Hi,
Look at the attached screenshots, one was taken from a mac (Sierra) and the other one Linux (Ubuntu). Linux is (more) correct about the sextuplet but also why are there duplicated notes ? This is the tree
?
(
((4 8) ( (2(1/2 1/2 1/2 1/2 1/2 1/2 1/2 )) (1(1/4 1/4 1/4 1/4 1/4 1/4 )) -1 ))
((4 8) ( (2(1/4 1/4 1/4 1/4 1/4 1/4 1/4 1/4 1/4 )) -1 -1 ))
)
I’m sure Karim has a great answer !
Cheers
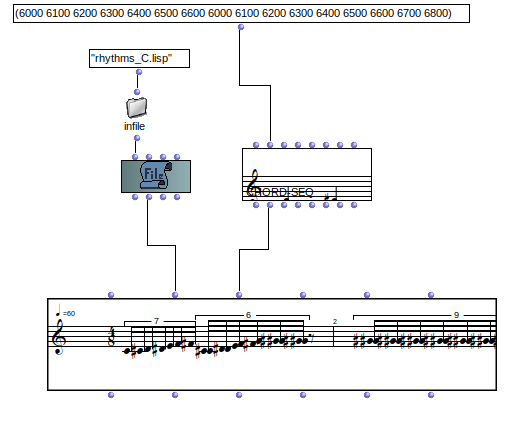
Hi Jaros,
[i have tested this on linux (om vers. 6.9.1b).]
First of all you should not use ratios in a tree. This could be a source of problem :
OM => (? (((4 8) ((2 (1/2 1/2 1/2 1/2 1/2 1/2 1/2)) (1 (1/4 1/4 1/4 1/4 1/4 1/4)) -1)) ((4 8) ((2 (1/4 1/4 1/4 1/4 1/4 1/4 1/4 1/4 1/4)) -1 -1))))
OM > Warning zero is not allowed in rhythm tree -> 0
Try to substitute it with this tree (same rhythm):
(? (((4 8) ((2 (1 1 1 1 1 1 1)) (1 (1 1 1 1 1 1)) -1)) ((4 8) ((2 (1 1 1 1 1 1 1 1 1)) -1 -1))))
Concerning no the repeated notes, this is simple. It is the method imbeded in voice, since you have less notes than pulses, voice will decide to repeat the last chord till the pulses are finished. If you need to change it or do something circular, yuo should repeat your chord series according to the num of pulses that you can have using n-pulses method.
Hope this answers your question.
Best wishes
K
Hi. As Karim points out the subdivisions should be stated as integers. The use of ratios also accounts for the extra notes appearing (through various heuristics searching for ties and quasi grace-notes).
-anders
Thank you Karim. I’m using 6.10.1 in Ubuntu.
Interesting that I don’t get the warning: OM > Warning zero is not allowed in rhythm tree -> 0
My listener does not complain, this is my output: OM => #<voice 24CA691F>
Regarding ratios:
"Proportions can be expressed with integers, floats or ratios. Nevertheless :
A same group cannot take both floats and ratios.
Values between 0 and 1 are not accepted by rhythm trees.
OM renders an approximation…"
This is OK but in the examples before that section under “Elementary Proportions Lists” ratios are used. So the above statement only applies to groups (? accordingly).
I think the place where this is very clear is in “Representation and Rendering of Rhythmic Structures”; also in OM Book 2
“An RT is defined by a couple (D S) where D is a fraction (>0) and S is a list of n elements defining n proportions of D. Each element of S is either an integer, or an RT”.
I think the OM documentation is confusing some times, but might be a translation problem. I guess.
Cheers
Hi there,
re: “no 0 in rhythm trees” – in general this is true, however in OM 6.10 this might be interpreted as a kind of “grace note” : you are allowed to form groups like (0 1 0), where the notes flagged with a 0 will not count in the rhythm and just be attached (with a slight offset) to the note with a 1.
This also explains why the chords are not similarly formed with 0s in the tree, depending on OM version.
=> with no 0 in the tree, both version should give you the same result 
Funny
Representation and Rendering of Rhythmic Structures is an article that I wrote with Carlos Agon. It is suppose to be an abstract concept and not specially for OM. For instance, if ideally you will use (4/4 ( 1 1 1 1)) to express a measure. But in lisp (and many other languages) once used so the compiler will calculate automaticaly the ratio 4/4 (time signature), and this will lead to problems. So we decided either we use 4//4 as time signature, or Exceptionnaly (4 4) for the time signature, and as you notice it is not an integer nor a ratio for D in an RT. This is only a convention for implementing it in OM.
It seems that recently RTs went to some changes that I disapprove partly because it just leads to incoherent and unstable rendering. But this is only my opinion. So an advice Chris, leave ratios and zeros alone concerning RTs and you will have a rather stable rhythm rendering. If you want to use grace-notes, Jean’s zeros system are ok starting from OM6.10 as he mentionned it.
Cheers
K
Very interesting topic indeed. Karim, I think in your article (2002) it is more than an abstract concept; it is a protocol but not a universal standard (obviously). Though, the abstract says: “This protocol has been implemented in the OM environment…”
Best