< Back to IRCAM Forum

Recursive Equations in OM6

OpenMusic
#1

Hello,

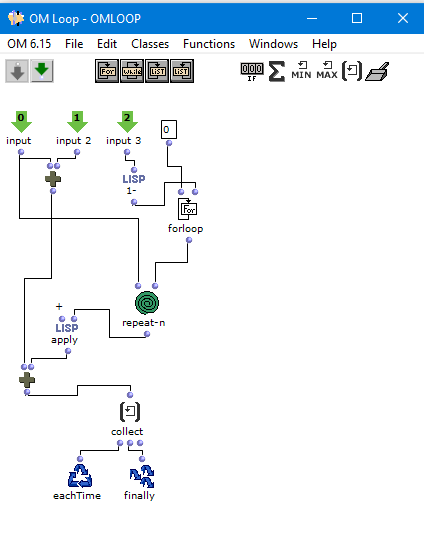
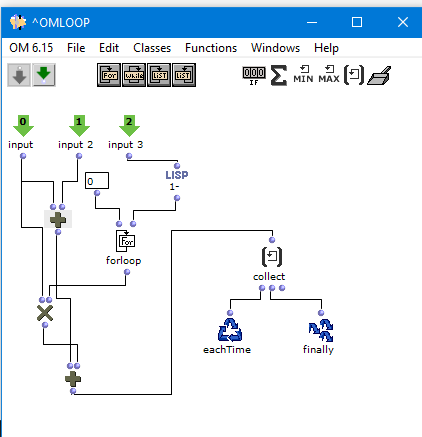
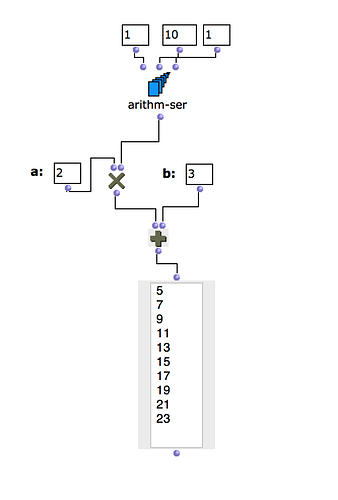
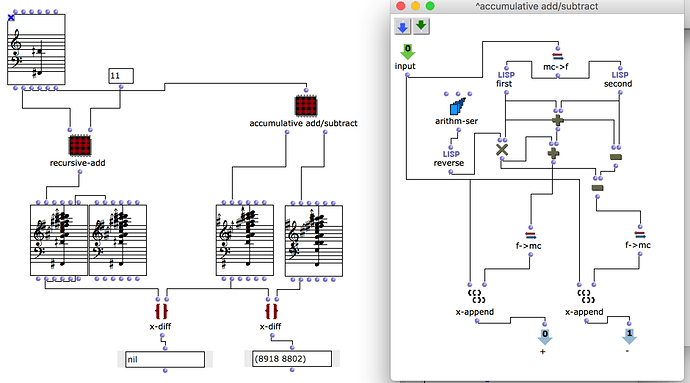
I’d be grateful for thoughts on how to create a patch for simple recursive equations in OM6. I’m not sure which path to take after looking through the forum and at omloop and tutorial 38 - I’m not so familiar with this side of OM but hoping it’s a trivial task.

I simply want to add two numbers, A to B, and then feed the result back to become B in the next iteration. So I expect I need 2-3 inputs (A and B or a list with them together, and the total number of recursions), and I want the patch output a list that collects the results of the addition for each iteration, so you get a+b, a+(a+b), a+(a+(a+b)) etc (it’s for a basic harmony technique like ring modulation).

Many thanks in advance for any pointers.

Cheers
Nick

#2

hello nick,
i’m not sure if this might help. but surely solves the problem. and there’s probably a better solution.
just check it out.
input: a, b, c (total number of recursions)

(lambda (a b c) (loop for i from 0 to (1- c) collect (om+ (apply '+ (repeat-n a i)) (+ a b))))

or

57
Screenshot 2019-08-30 03.13.57.png424×536 8.8 KB

kind regards,
perti

#3

Many thanks Perti, that looks great.
One question: I’m not sure exactly what’s inside the ‘repeat-n’ omloop as I don’t understand the lisp line you wrote / don’t know lisp itself. Could you clarify it in terms of patching? Thanks in advance!
N

#4

ok nick, i’ll try. english is not my first language so it might be a bit confusing at times.
repeat-n has two inputs: one for ‘how many’ and the other for ‘what’.
you asked for a+b, a+(a+b), a+(a+(a+b))… you can see that ‘a’ is cumulative in each iteration
so, in each iteration in the repeat-n makes a list of repeated a’s which and applying '+ to all elements returns total sum of a’s. i’m not really sure why i put it this way as it is more logical to multiply ‘a’ by the count of cycles in the loop. in this way,
(lambda (a b c) (loop for i from 0 to (1- c) collect (om+ (* i a) (+ a b))))
perhaps because it was late in the evening, but it seems i took a less direct way to solve it. sorry about that. but as i always have thought when programming, right results come first, then comes efficiency and elegance (the difficult part).
19
hope is clearer now.
regards,
perti

#5

Hi nm0, hi perti,

as the problem has been sketched out, i suppose a and b are single numbers (not lists).
Then in fact the operation is equivalent to: 1a+b, 2a+b, 3a+b…
which would simply go something like this:

07
Screen Shot 2019-08-30 at 20.56.07.png666×984 16.7 KB

If a = {a1, …an} and b = constant then recursion would be appropriate:
a1+b, a2+(a1+b), a3+(a2+(a1+b),…
?

#6

and there it is!.. efficiency and elegance.
thanks for a more logical thought.
best,
perti

#7

Thanks Perti - it works perfectly! I appreciate your insight and elegant solution.

Attached is the actually patch, a simple recursive additive frequency harmonic device.

Many thanks
Nick

recursive-rm.omp (14.5 KB)

#8

Cheers Pre, even simpler. I’ll try this implementation too since I want to also make a subtractive version.
Nick

#9

hi perti,

i think this is the idea behind the OM-versions of arithmetic operators, that you can apply them on lists not only atoms, as with the genuin lisp versions…

hi nick,
i hope thats equivalent to what you did in your patch… i am a bit to tired to check that today…

best
pre

#10

44
Screen Shot 2019-08-30 at 22.29.44.png1880×1044 90.2 KB

#11

Amazing, thanks for that, I’ll see if i can also do subtraction with your simpler method above, but this looks great in any case
Cheers
Nick

#12

I was curious about the different effects of addition and subtraction, so i already did it on the second output. In fact the difference is just 2 pitches… see x-diff
…?

Anyway, happy chord-finding
Best
Pre

#13

I’d also be curious to ask you both and anyone else - how did you learn about omloop and related features in OM?

I’m asking since I personally don’t find the manual so clear to get started with this topic, but I imagine this is because I’m not familiar with lisp nor computing/maths enough to get the gist of it by myself. The principles seem straight forward once I see example patches but the manual isn’t so user friendly for beginners, I feel.

#14

In my experience:
Good books/websites to go deeper into lisp, but not necessarily always for quickly solving a problem:

#15

Many thanks! I’ll take a look at those.
N

#16

hi nick,

i learned lisp loop firstly (but not deeply enough), then after some research here and there and a lot of effort i came to know (again not entirely) omloop. sometimes i find one preferable over the other, depending on the situation. but who knows why i tend to think more in terms of looping instead of other tools like apply or funcall.
i concur with the bibliography provided by pre. chapter 22 of seibel’s book (loop for black belts) helped me a lot.
i’m not a programmer but a musician with programming needs, though.
cheers,
perti

#17

rethinking your problem: maybe this is the kind of modulation you had in mind…

25
Screen Shot 2019-08-31 at 10.51.25.png2190×1520 216 KB

harm. ser. modulated.omp (18.0 KB)

happy weekend
pre