Permutations - lisp code to hack a function

[krhes]

Greetings All,

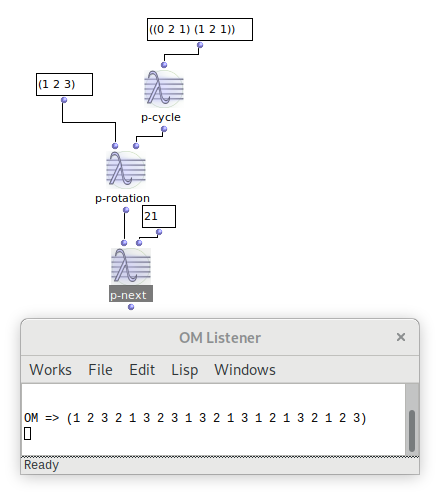
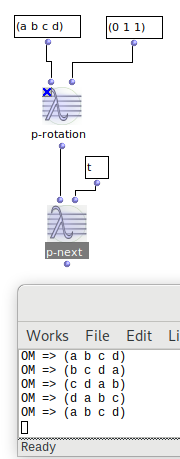
I have a question about permutations (the function) which I was hoping to code hack to determine the path that the permutations would take. Ideally, instead of using permutation to generate:

((1 2 3)
(1 3 2)
(2 1 3)
(2 3 1)
(3 1 2)
(3 2 1)).

I would like the following:
((123)
(213)
(231)
(321)
(312)
(132)
(123))

The following steps would be useful to be able to control: let a = swap adjacent pairs, b = swap individual (specified) pairs, c = an integer to remain unchanged in the next permutation (eg. (132) (123)) and then be able to recall the original sublist (in the above case (123)) at the end. My lisp skills are rudimentary to put it kindly, but I’m sure this kind of recursive permutation is perfect for lisp. Would anyone be able to help? To be able to control adjacent pair swapping would help if nothing else. With the above a,b,c & d I would also be able to generate the following (for instance):

123
132
312
321
231
213
123

and of course scale up to any number of integers in a list.

Thanks in advance,
Krhes

[anders]

Hi Krhes.

The ‘Patterns’ library gives you access to all sorts of ways to structure patterns of data and generate automata, from standard things like cycles, series, weighted random, markov chains etc, - to more explicit orderings, like graphs, rewrite-systems (L-systems), and useful in your particular case - rotation patterns. It comes with a set of tutorials which hopefully describes the various approaches. Check the attached screenshot for an example returning the sequence you’re using as an example.

[krhes]

Good morning Anders,

This is perfect!! I’m looking forward to exploring this library (though I should pursue greater knowledge of lisp too!).

My sincere thanks,
Krhes

[anders]

though I should pursue greater knowledge of lisp too!

Agreed. Besides being very useful, it’s also great fun! But it’s difficult to give any advice or provide specific help here, you’ll find much online learning material however, surely something which fits your needs. One of the greatest things with OM is all Common Lisp is there at all times, so if you want to check some code in some book or similar, just do it.

OM by itself, although not aimed that way, is obviously also a great resource. Most code in OM is well structured and documented. Hitting ‘e’ on an object jumpt to the code, and probably most of OM’s end-user various functions, classes etc. are not too hard to grab.

In the case of #'permutations it’s perhaps not a very complicated function, but this of course depends on the reader.

[krhes]

Dear Anders,

I’m really happy with patterns so far and I have barely scratched the surface!! Thank you again for making this library known to me.
Not wanting to prove the old Chinese proverb - "If you save a life, you responsible for that life’ I did, however, wonder if you could explain/make totally clear the process behind swapping process in permutations. For a moment I thought I understood start, step, width but now it alludes me. For eg. I understand (011) - integer in position 1 moves to 3, integers in positions 2 & 3 move to 1 & 2. However seeing the shapes is not the same as understanding the underlying reason. Secondly, how does the nested list, for example ((0 2 1 )(1 2 1)), work ie. how does it map its structure and permute a list?
Sincerely hoping this old dog can learn new tricks, and thanks in advance,
Krhes

[anders]

Hi Krhes.

if you could explain/make totally clear the process behind swapping process

Together with the general documentation of the Patterns-lib, the rotation pattern is hopefully well explained in the accompanying tutorial file “009 a rotation”.

One of the nice things about the Patterns lib is that items and data, but also patterns and parameters can be nested arbitrarily, and be provided as patterns or sub-patterns themselves. Such is also the case in the example, where ((0 2 1)(1 2 1)) is input to a 'p-cycle pattern before being passed on to control the ‘rotation’-pattern. The p-cycle pattern returns a cycle of the elements in its input (possibly with sub-patterns included).

So for the first generation of the pattern, the rotation parameters (0 2 1) is used, the second (1 2 1), the third back to (0 2 1) and so on. If you bypass the p-cycle, and input each of the ‘rotation specs’ - ie. (1 2 1) or (0 2 1) - to the p-rotation pattern, it’s perhaps easier to see what’s going on.

To easier step or debug what’s going on you can try passing ‘t’ as the input to 'p-next’s parameter, then it will return one generation for each evaluation (just take care to lock the pattern after the first evaluation, or else you’ll start anew each time). Check attached.

[krhes]

I really appreciate your time and effort explaining this, Anders - thank you so much. Will dig in later!
Kind regards,
Krhes.