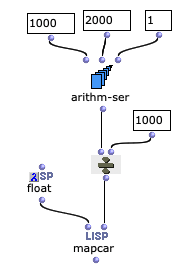
Hi -
I understand from an old post that part of the strange behaviour of arithm-ser with floats is to do with floats estimation in Lisp. (Maybe it converts to rational and then back again?) But is the function meant to behave in this way?..
With this:
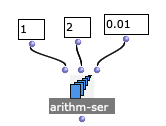
The output is:
(1 1.01 1.02 1.03 1.04 1.05 1.06 1.0699999 1.0799999 1.0899999 1.0999999 1.1099999 1.1199999 1.1299999 1.1399999 1.1499999 1.1599999 1.1699998 1.1799998 1.1899998 1.1999998 1.2099998 1.2199998 1.2299998 1.2399998 1.2499998 1.2599998 1.2699998 1.2799997 1.2899997 1.2999997 1.3099997 1.3199997 1.3299997 1.3399997 1.3499997 1.3599997 1.3699997 1.3799996 1.3899996 1.3999996 1.4099996 1.4199996 1.4299996 1.4399996 1.4499996 1.4599996 1.4699996 1.4799996 1.4899995 1.4999995 1.5099995 1.5199995 1.5299995 1.5399995 1.5499995 1.5599995 1.5699995 1.5799995 1.5899994 1.5999994 1.6099994 1.6199994 1.6299994 1.6399994 1.6499994 1.6599994 1.6699994 1.6799994 1.6899994 1.6999993 1.7099993 1.7199993 1.7299993 1.7399993 1.7499993 1.7599993 1.7699993 1.7799993 1.7899993 1.7999992 1.8099992 1.8199992 1.8299992 1.8399992 1.8499992 1.8599992 1.8699992 1.8799992 1.8899992 1.8999992 1.9099991 1.9199991 1.9299991 1.9399991 1.9499991 1.9599991 1.9699991 1.9799991 1.989999 1.999999)
Not ideal, but could be rounded. And length of the list is 101, as expected for 1 to 2 inclusive.
But… Change the incrementor to 0.001:
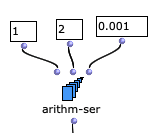
It will still need rounding, but worse is that the length of the list is 1000 when it should be 1001.
That can be remedied by changing the end value to 2.001, but that doesn’t seem like the right place to be cajoling it into behaving as needed.
Shouldn’t arithm-ser behave consistently, and also output incremented values as expected rather than needing rounding. Maybe if there were a precision argument so that it allows for the estimated version too…?
Thanks!
Graham