Bonjour Jérôme,
La notion d’OIS de Stephen Heinemann est vraiment très pratique pour effectuer une opération de multiplication d’accords de façon manuelle, sur papier mais aussi en utilisant les opérateurs modulo 12 (Zn-mod- et Zn-mod+) de la librairie Mathtools, Mathtools ou dans le groupe Dn, il y a aussi la fonction dédiée Zn-transp-comb qui permet de calculer directement la multiplication d’accords entre deux ECH ou un ECH A et un OIS B, les résultats étant semblables.
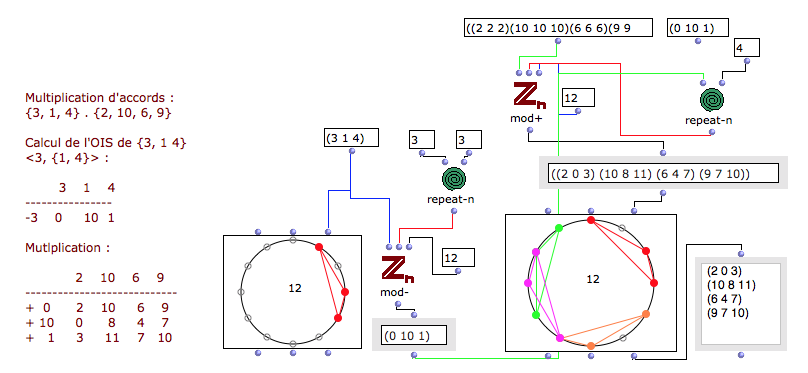
Concernant l’OIS, en reprenant l’exemple XIII bis de Pierre Boulez donné dans Relevé d’apprenti et le chapitre Eventuellement - {3, 1, 4} . {2, 10, 6, 9} - on se rend compte que d’une part dans l’ECH {3, 1, 4} c’est le calcul des intervalles entre la première hauteur et toutes celles du premier bloc sonore, et y compris elle-même, ce qui permet, de fait, de transposer l’ECH sur une base de do {3, 1 4} => <3, {1, 4}.
Perso, je trouve que la formulation <3, {1, 4}> est déjà explicite en elle-même pour un utilisateur pas forcément “matheux”. Ensuite, le calcul est d’une simplicité biblique. La première hauteur est mise en exergue en l’isolant des autres. Elle indique le nombre en demi-tons qu’il faut pour transposer l’ECH sur la base de do, soit 0. Ici, il s’agit de mib ou ré# soit -3. L’opération, très simple, s’effectue modulo 12 comme ci-dessous :
3 1 4
-3 0 10 1 l’OIS = 0, 10, 1
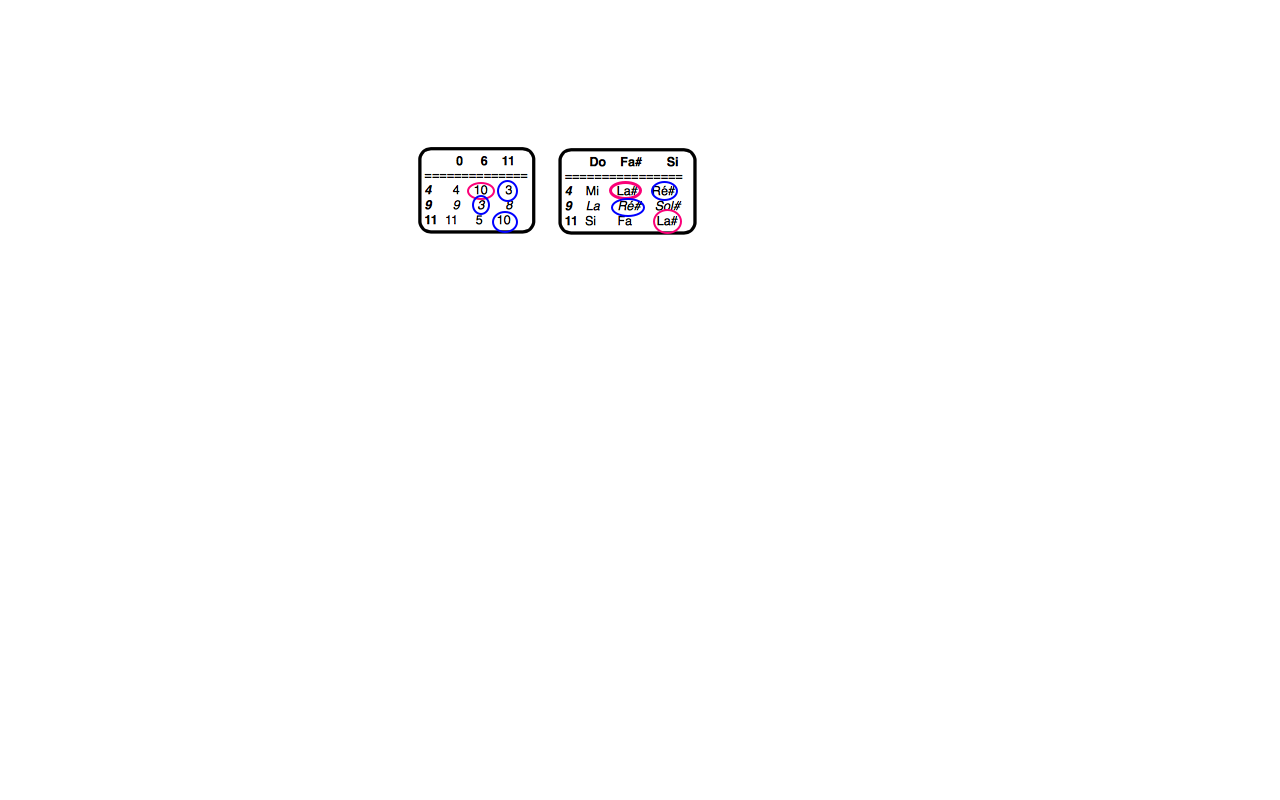
Dès lors, cette multiplication, que certains décrivent comme étant une opération complexe, est aisée. Elle consiste à reporter chacun des intervalles de l’ECH {3, 1, 4} sur chacune des hauteurs de l’ECH {2, 10, 6, 9}. Ces dernières hauteurs étant introduites dans le résultat de l’opération modulo 12 grâce à l’OIS et la transposition du do, soit 0 :
2 10 6 9 ----------------------------
- 0 2 10 6 9
- 10 0 8 4 7
- 1 3 11 7 10
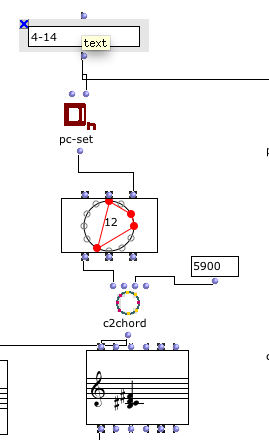
Il suffit de reporter le résultat en enlevant les doublons 7 et 10 et on obtient le résultat de Pierre Boulez. J’ai fait un PDF avec des copies d’écran qui expliquent pas à pas ces opérations “manuellement” ou en simulant le calcul manuel avec les opérateurs d’OM et confirmées avec le résultat de Zn-transp-comb. Et je mets aussi en pièce jointe le fichier OM.
Ceci étant, la thèse de Stephen Heinemann est très intéressante à lire, elle donne beaucoup de clés de compréhension sur les diff:érentes opérations modulo 12.
Didier
PS : Désolé pour les calculs en “matrice”, la mise en page m’enlève les espaces. Résultat ce n’est pas très lisible. Dès lors, il faut se référer au PDF.