Help with constraint problem

[zeracosaitam1]

Hi! I come with a problem that unfortunately needs some explaining

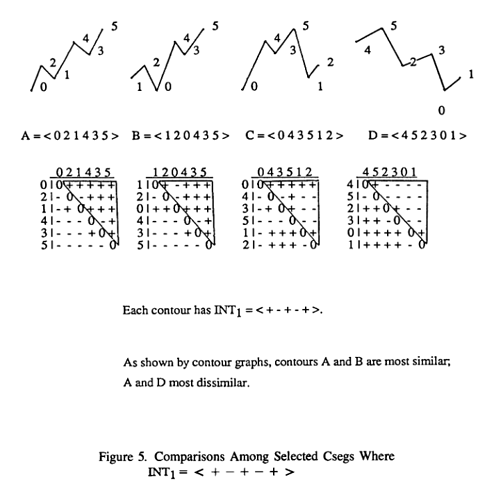
I’ve been exploring contour-segment theory, a field that analyzes melodic contours by focusing on the relative highness or lowness of pitches over time, rather than their exact intervals or pitch classes.

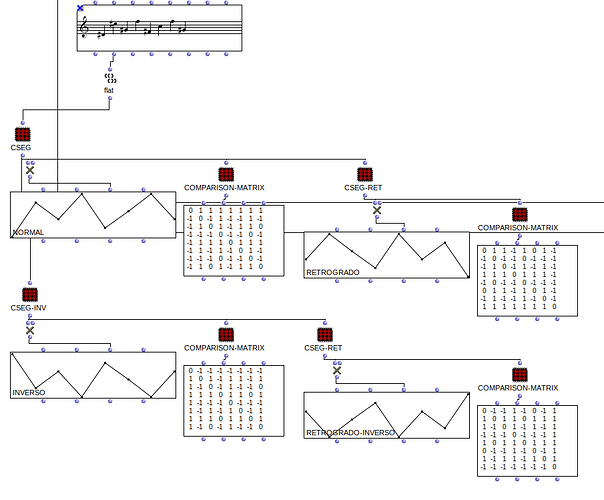
I managed to make a patch that generates these “c-segs” and its transformations (i realized this specific thing was already possible with BPF tools but it was fun to patch).

I also managed to patch a COM-matrix, that is a comparison matrix that checks each point in a contour against all others and outputs:

• 1 if the point is higher
• -1 if it’s lower,
• 0 if they’re equal.

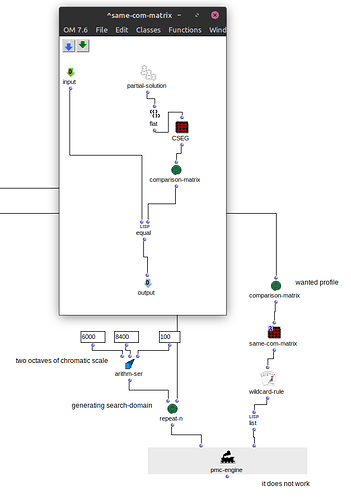
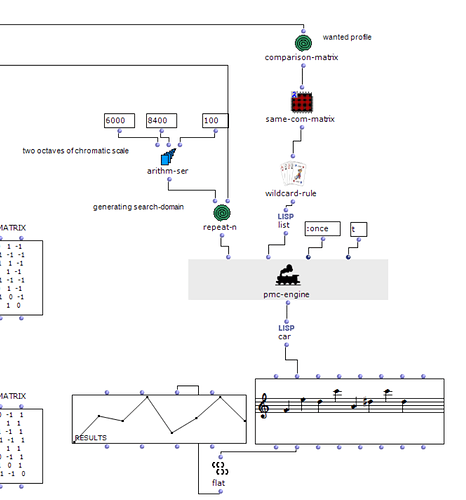
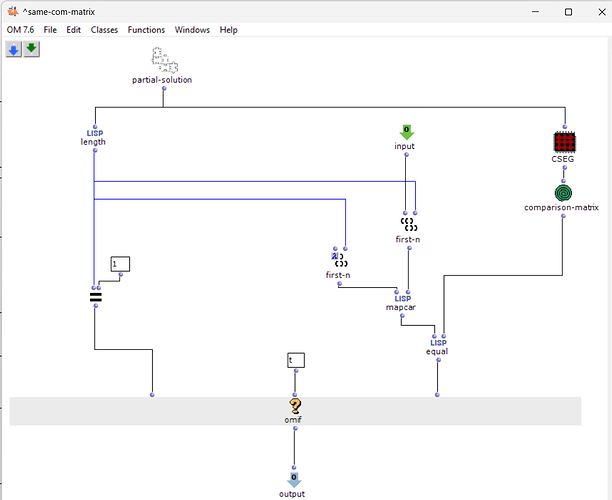
The thing i’m having problems is, I want to program a patch that would generate a random but valid melody that corresponds to a given COM-matrix

The first thing that came to mind to achieve this was using constraint programming. I tried to make something with OMCS, writing a constraint that computes the COM-matrix of a partial solution and checks it against a given target matrix. This did not work (it always returned nil) as i later learned that OMCS applies the constraint to each candidate as it builds the solution up, and the com-matrix being a global property, the constraint could never be met. So insisting on this route would mean I’d need to use the entire set of permutations of X pitch values as the search domain, and that would be absurd

So, is this possible to achieve with some other strategy? Or is it not feasible?

Here’s the patch:

CSEG.omp (73.5 KB)

Thanks for your time, as always!

[haddad]

Hi,

Interesting problem, though it lacks some more specific description of the problem. Ehat do you mean by valid here:

@zeracosaitam1

generate a random but valid melody that corresponds to a given COM-matrix

i,e what’s valid or not for you.

I will take a look on your patch and get back to you.

BEst
K

[zeracosaitam1]

Hi K!

Reading again you’re right i was not clear enough

With valid I meant a melody that has the same comparison matrix as the one I define (i.e. has the same relative heights between all points).

This was inspired by this part of the essay (“Relating Musical Contours: Extensions of a Theory for Contour” by Marvin & Laprade, if you’re interested), where they explain how the COM-matrix can be used to compare melodies with the same progression of adjacent relative heights:

INT1 refers to the first diagonal after the 0s, they describe the relative heights between adjacent points, INT2 describes the relative heights between every other point, INT3 between every third point, etc

In the essay they use this tool to analyze and compare contours in music but I started wondering if it could not be used as a generative tool also. It interests me very much the possibility of defining contours from a matrix (where i can’t exactly tell what the contour would result in, but have much more control on the similarity or difference between contours) instead of writing the exact pitches or drawing in a BPF.

Anyways, I hope it’s clearer now, thanks for helping me out, as always

[haddad]

Ok, thank you this is much clearer for me now. (I am sorry didn’t know about this theory).

At first sight, (i should first read the article) I don’t think it is a good idea to use constraint programing to generate a random matrix of this sort. Constraint programing mainly aims to solve a certain computational problem. And the most important point in this kind of programing is to have a perfect definition of the given problem as rules. Otherwise it could lead to wild and interminable calculations leading to a dead end.
So my advise here is that before asking yourself what kind of computational approach you will be using, is to well determine your problem. You will find yourself better off and even find that you may not have even to use this sort of programing, but rather another one. At least this would be my way to deal with this kind of problem.

Best
Karim

[paulohgraposo]

Hello zeracosaitam1 and Karim,

I hope you’re doing well!

Sorry for jumping in like this, but I made a few tweaks to the patch you sent and I think it’s now working properly with the OMCS library.

This is the internal patch:

Just to give you a quick rundown of what I did:

The “partial-solution” tool always starts with a single variable, and then others are added one by one—forming lists of 2 variables, 3 variables, and so on. So, the constraint needs to adjust to different list sizes.

First things first: if the list only has one variable, we just get “t.” That’s because you can’t really calculate an interval with a single note. So, this restriction only kicks in when there are at least two variables.

Next, I used the “first-n” function to pull the first two lists from the matrix and then “mapcar → first-n” to grab just the first two values of those lists. That way, we can compare the first two notes, then the first three notes, and so on.

Here’s a quick example—say we have a list with two variables in “partial-solution,” using this matrix:

(0 -1 -1 -1 -1 -1 -1 -1)  
(1 0 1 -1 1 1 -1 1)  
(1 -1 0 -1 1 -1 -1 0)  
(1 1 1 0 1 1 0 1)  
(1 -1 -1 -1 0 -1 -1 -1)  
(1 -1 1 -1 1 0 -1 1)  
(1 1 1 0 1 1 0 1)  
(1 -1 0 -1 1 -1 -1 0)  

First, we select the first two lists (“first-n”):

((0 -1 -1 -1 -1 -1 -1 -1) (1 0 1 -1 1 1 -1 1))  

Then, from these two lists, we extract only the first two values (“mapcar → first-n”):

((0 -1) (1 0))  

Now, “t” will only be returned when the omloop patch “comparison-matrix” matches this list exactly.

Once this restriction is met for two notes, the process continues, testing progressively larger lists.

This step-by-step approach is important because, with 8 variables, each having a domain of 25 notes, we’re dealing with more than 1.5 trillion possibilities—which is quite the beast! By breaking it down into stages, the computation becomes manageable.

I’m attaching the patch — i hope that it works!

cseg-v2.omp (79.9 KB)

Best,
Paulo

[zeracosaitam1]

Hi Paulo!

It works perfectly! Thank you for the detailed explanation btw, it gave me a better feel of how to approach these kind of problems with CS, cheers!