Hello! I came up with this process:
It starts with a polyrhythm of N different pulses, and it takes every ‘coincidence point’ between pulses (marked with arrows) and applies a circular rotation “vertically” (like the examples below the grid)
I’m having trouble finding a way to iteratively apply this pattern, specially in finding a way to make OM recognize ‘coincidence points’ and apply some pattern to it. Any tip or nudge in the right direction would be greatly appreciated! Thank you!
Cool!
Out of my head - the “rotation”-pattern in the Patterns lib will give you an endless rotation stream, with any given “rotation-pattern”
You can specify a fixed rotation pattern, or a pattern which changes over time. Or perhaps in your case providing a lambda-patch - which changes the rotation-pattern according to the current state of the pattern as input - ie. checking for coincidence points.
Seems your problem is something close to the “change ringing” techniques of tolling church bells for maximum diversity = min repetition?
I’d love to know what kind of good solutions you end up with!
-anders
I’d like to do some attempts using the Patterns techniques, but can’t promise anything soon…
Dear zeracosaitam1
Here is a possible solution to output the pulses with their respective “coincidence point”:
of course it is even easier in code.
Here is the folder (patch + lisp lambda functio) to unzip and import in OM’s workspace:
polystuff.zip (3.0 KB)
Best
K
Oh how interesting, just the other day I became fascinated with change ringing, precisely because of that brief mention in Notes From the Metalevel haha. I’ll take a look, it’s a shame because I find that library absolutely perfect for much of my workflow but i still can’t grasp a lot of it’s functionality, It feels so different to anything else inside OM.
Hi Karim, thanks as always for the help!
Your solution works like a charm, the only thing that i realized i should have included in the photo (just to clarify what i want to achieve) is that i start with each ‘voice’ playing just one pulse (here with a different example):
However, your patch still works when i input just the pulses, like so:
(3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3)
(4 4 4 4 4 4 4 4 4 4 4 4 4 4 4)
(5 5 5 5 5 5 5 5 5 5 5 5)
(6 6 6 6 6 6 6 6 6 6)
The problem now is that the list does not take into account which voice is playing which pulse in each step, but i’ll see if i can solve it on my own 
I’ll come back if i become stuck or find a good solution 
Thank you!
Hi everyone,
I finally had some free time to return to this.
While analyzing Karim’s patch, I realized that the output of the omloop3 is almost what I wanted. The only thing missing is the rotation of the non-nil values (while preserving the nil values’ positions) to then perform a mat-trans to get a final list of time intervals per voice.
I found a partial solution using some custom Lisp functions with the help of ChatGPT, contained inside the ‘rotation’ loop.
The only issue is with the nature of the rotation. Currently, the rotation is applied to each original element that gets inputted into the rotation loop, always in its original position. However, I want the rotation to be applied iteratively to each element as it gets rotated, so it should ‘remember’ the new positions of the elements as it continues rotating.
This general problem of iteratively applying a process recursively to the output of the same process keeps confusing me. I don’t yet understand how to patch such things. I hope I explained myself clearly enough, english is not my native language 
Any tip or help will be greatly appreciated!
polyur2.omp (19.4 KB)
Hi,
Have you tried OM’s circle (n-cercle) representation? you can easily plot euclidean (poly)rhythms with them.
All the best,
António
Hi Antonio,
No, I haven’t tried that yet!
The process I’m working on doesn’t involve Euclidean rhythms though, or at least I don’t think it does.
What’s troubling me right now is figuring out how to use the output of a loop as the input for the same loop. I’m trying to use ‘acum,’ but it gets confusing when processing complex lists. How do people usually deal with these cases?
I’ve found an alternative method to identify where multiple pulses coincide by calculating the LCM of each possible combination of the pulses I’m using, so that’s another approach.
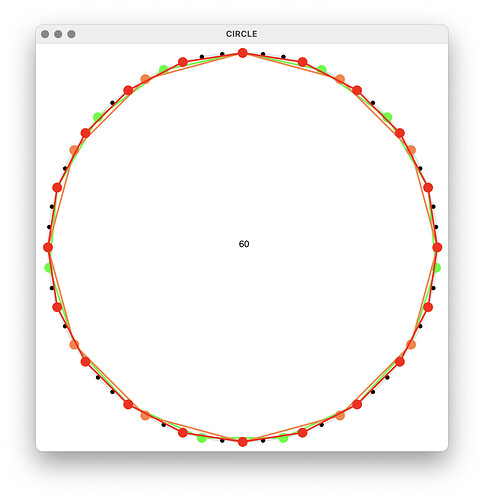
Maybe I should explain what was the musical idea behind this. The idea was to play a certain polyrhythm and use all the coincidence points to interchange the voices falling on the same spot, creating more varied rhythms for each voice. The overall sound would still be the same polyrhythm, but with a kind of hocket logic.
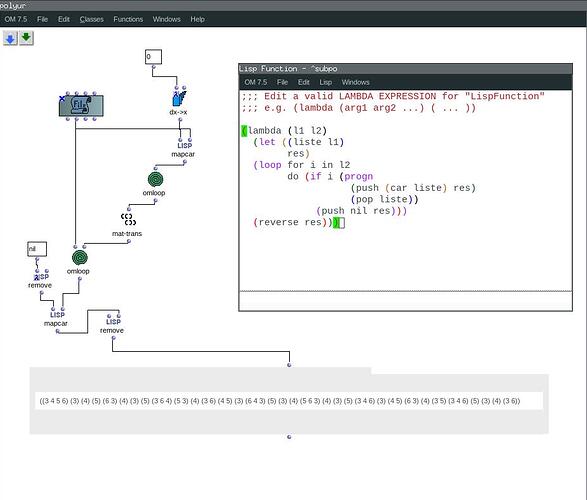
Now it’s almost solved thanks to Karim’s patch. His patch (the output of omloop3 specifically) returns lists of this kind:
((2 3 4 5 6) (2 nil nil nil nil) (nil 3 nil nil nil) (2 nil 4 nil nil) (nil nil nil 5 nil) (2 3 nil nil 6) (2 nil 4 nil nil) (nil 3 nil nil nil) (2 nil nil 5 nil) (2 3 4 nil 6) (2 nil nil nil nil) (nil 3 nil 5 nil) (2 nil 4 nil nil) (2 3 nil nil 6) (2 nil 4 5 nil) (nil 3 nil nil nil) (2 nil nil nil nil) (2 3 4 nil 6) (nil nil nil 5 nil) (2 nil nil nil nil) (nil 3 nil nil nil) (2 nil 4 nil nil) (2 3 nil 5 6) (2 nil 4 nil nil) (nil 3 nil nil nil) (2 nil nil nil nil) (nil nil nil 5 nil) (2 3 4 nil 6) (2 nil nil nil nil) (nil 3 nil nil nil) (2 nil 4 5 nil) (2 3 nil nil 6) (2 nil 4 nil nil) (nil 3 nil 5 nil) (2 nil nil nil nil) (2 3 4 nil 6) (2 nil nil 5 nil) (nil 3 nil nil nil) (2 nil 4 nil nil) (2 3 nil nil 6) (nil nil nil 5 nil) (2 nil 4 nil nil) (nil 3 nil nil nil) (2 nil nil nil nil) (nil nil nil nil nil))
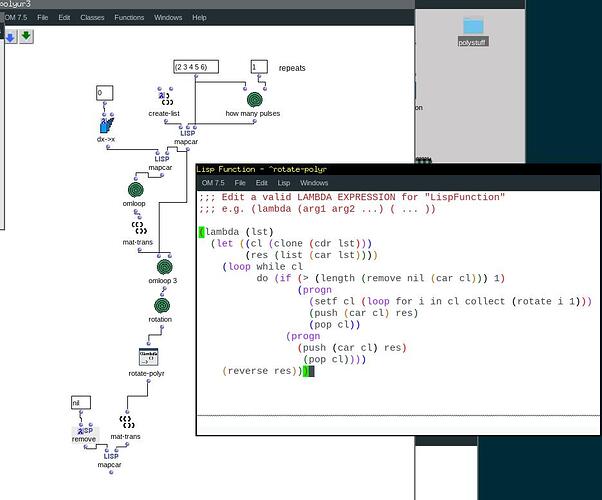
that tracks where each pulse will fall in each step. I managed to kind-of patch the next step, the rotation part (the rotation loop in the patch i shared), but the rotation is applied to each step independently (the asteriks are mine, to mark some of the places where a rotation is applied):
((6 2 3 4 5) (2 nil nil nil nil) (nil 3 nil nil nil) *(4 nil 2 nil nil)* (nil nil nil 5 nil) *(6 2 nil nil 3)* *(4 nil 2 nil nil)* (nil 3 nil nil nil) *(5 nil nil 2 nil)* *(6 2 3 nil 4)* (2 nil nil nil nil) *(nil 5 nil 3 nil)* *(4 nil 2 nil nil)* (6 2 nil nil 3) (5 nil 2 4 nil) (nil 3 nil nil nil) (2 nil nil nil nil) (6 2 3 nil 4) (nil nil nil 5 nil) (2 nil nil nil nil) (nil 3 nil nil nil) (4 nil 2 nil nil) (6 2 nil 3 5) (4 nil 2 nil nil) (nil 3 nil nil nil) (2 nil nil nil nil) (nil nil nil 5 nil) (6 2 3 nil 4) (2 nil nil nil nil) (nil 3 nil nil nil) (5 nil 2 4 nil) (6 2 nil nil 3) (4 nil 2 nil nil) (nil 5 nil 3 nil) (2 nil nil nil nil) (6 2 3 nil 4) (5 nil nil 2 nil) (nil 3 nil nil nil) (4 nil 2 nil nil) (6 2 nil nil 3) (nil nil nil 5 nil) (4 nil 2 nil nil) (nil 3 nil nil nil) (2 nil nil nil nil) (nil nil nil nil nil))
The problem here is that the new order of the rotated elements is not remembered from sublist to sublist. So i think i need a loop that process the list entirely. That is to say, that if I have to rotate the 2-row (in this case index 0 of each sublist) with the 4-row (index 2), the loop should rotate these places in the whole list, and then update the positions of where is the 2-row now, where is the 3-row now, etc, before applying the loop again to this processed list.
I thought of using a list of pairs, where one element tells you to which row each pulse belongs, followed by the pulse in question, but the resulting list makes my head hurt 
Hi
I plotted these in a circle:
Whatever regular compound beats you come up with, you can find a n-beat circle which plots them. The number of beats n here is given by the least common multiplier of 3, 4, and 5.
All the best,
António
Connect the left-most outlet of accum to a collect, and connect collect to eachTime and finally in the usual way. At least that’s how I did it in order to solve that issue recently.
Dear zeracosaitam1,
If i understand you well:
Whenever there is 2 or more congruent pulses on a beat you want to do a rotation transforming displacing all voices starting from that beat. Then so on ?
Best
K
Hi Karim,
Yes, thats it!
Dear zeracosaitam1,
sorry for the late reply. Here is what i believe you want to achieve
Writing the code in lisp seemed to me easier.
And here is the folder with the patches:
rotation.zip (3.9 KB)
Best reagrds
K
