Hi,
sharing a simple implementation of FFT in OM and OM# (in Visual Programming). I believe it can be convenient when we are teaching or trying to understand FFT and Audio Processing.
Download: More->Download
If you find something weird let me know!
cheers! 
Hi Charles,
It would be great if there was an implementation of discrete Fourier transforms (DFT) over Z12 (24, 48, etc.), given how many direct music-theory applications of it have emerged over the last few years.
Is there a way of eliminating the constraint on N being a power of 2 on your patch? Without that constraint, it would be easy to apply it to Z12 (24, 48, etc.)
All the best,
António
Hi antonio,
The constraint of N power of 2 is just for FFT, for DFT you can use what you want, but it is much slower (very very much slow).
I have the patch for DFT in OM#, but not in OM (will be the same).
DFT.opat (103.6 KB)
Hi Charles,
with DFT.opat, I’ve unknown functions:
[!!] :: unknown function: i-number
[!!] :: unknown function: pi-number
[!!] :: unknown function: euler-number
why ?
Best,
Jerome
Hi Charles,
Thank you for the patch. I’ve just tested it with {1,0,0,0,1,0,0,1,0,0,0,0} (C major triad in Z12) and I’m not getting the expected results (beyond the first coefficient which gives the chord’s cardinality.) I should be getting:
{3. + 0. I, -0.366025 - 0.366025 I, 1. + 0. I, 2. + 1. I,
0. - 1.73205 I, 1.36603 + 1.36603 I, 1. + 0. I, 1.36603 - 1.36603 I,
0. + 1.73205 I, 2. - 1. I, 1. + 0. I, -0.366025 + 0.366025 I}
Instead, in OM#'s text buffer I’m getting:
#C(3.0D0 0.0D0)
#C(-0.3097215450815076D0 -2.452499622274118D-7)
#C(0.7153705256507716D0 -1.0659573879134854D-7)
#C(2.682506900001707D0 9.451659902515175D-7)
#C(-0.9189860623311323D0 -1.4373475367701616D-6)
#C(1.830830490544622D0 7.778796458079995D-7)
#C(1.830829468553722D0 9.334544273098544D-7)
#C(-0.918985745797471D0 -2.5153577749015277D-6)
#C(2.6825075074213225D0 2.5204435497583333D-6)
#C(0.7153694135659215D0 -4.796826983399782D-7)
#C(-0.3097206959784812D0 -2.452498031102479D-6)
#C(2.999999999995442D0 4.119577314857738D-6)
Am I missing something?
All the best,
António
Sorry, I forgot these objects.
euler-number is exp 1.
i-number is srqt -1.
and pi is pi. You can use eval pi.
All this are in OM-CKN (it needs OM-py) - without documentation for know.
DFT.opat (104.4 KB)
I can not say if you are missing something or not because I did not understand what you want rsrs.
How did you get these:
{3. + 0. I, -0.366025 - 0.366025 I, 1. + 0. I, 2. + 1. I,
0. - 1.73205 I, 1.36603 + 1.36603 I, 1. + 0. I, 1.36603 - 1.36603 I,
0. + 1.73205 I, 2. - 1. I, 1. + 0. I, -0.366025 + 0.366025 I}
The numbers I gave are correct. I computed them with Mathematica, and I can also compute them with bach (package) for MaxMSP.
Well, I do not know. If bach uses FFT, for example, it will add 0 at the end of the {1,0,0,0,1,0,0,1,0,0,0,0}. So it will be calculated something like that {1,0,0,0,1,0,0,1,0,0,0,0,0,0,0,0} what could change the final result.
But this is a guess!
No, both bach and Mathematica calculate the DFT and neither add zeros in order to make it a power of two. For some reason the numbers that I’m getting from your patch don’t match, but the numbers that I gave are 100% correct (you can even find them plotted in published articles, e.g. Callender’s Continuous Harmonic Spaces.)
Ok,
So don’t use it for your calculations.
I could not find any error in the implementation of DFT, but please, if you find some error let me know.
If you want to share your max patch I can give a look.
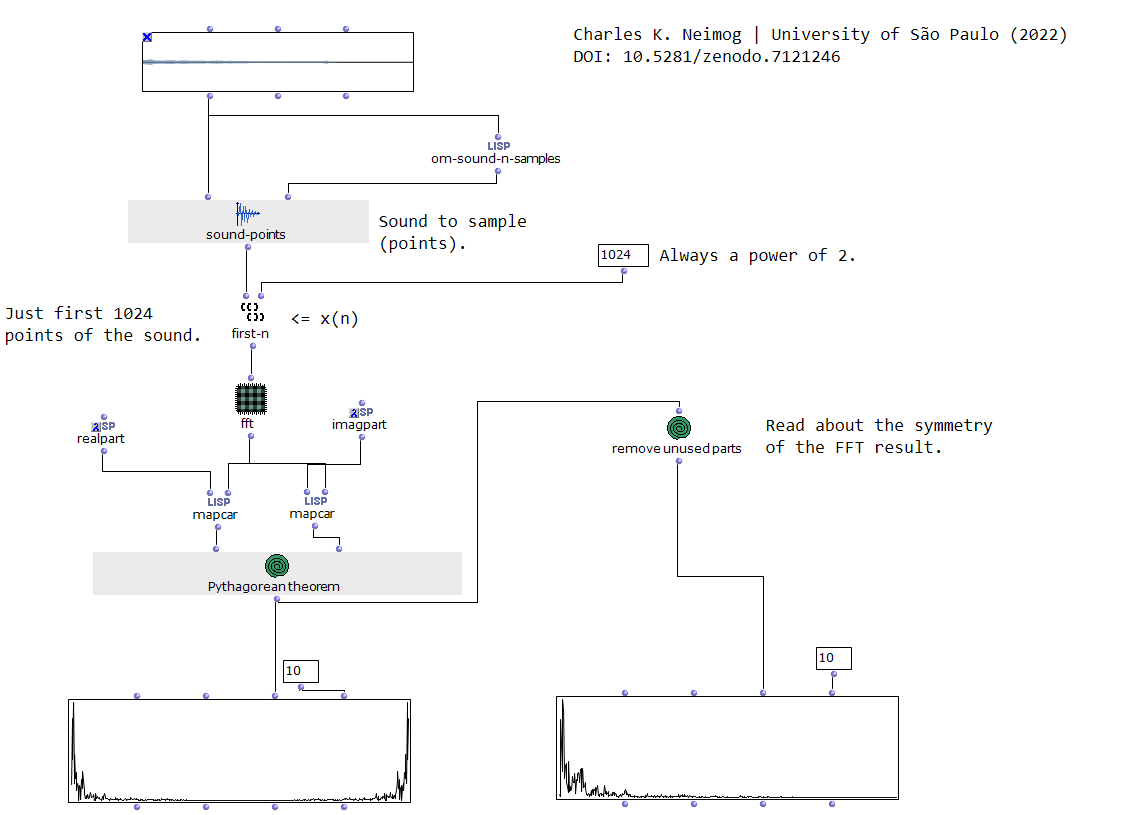
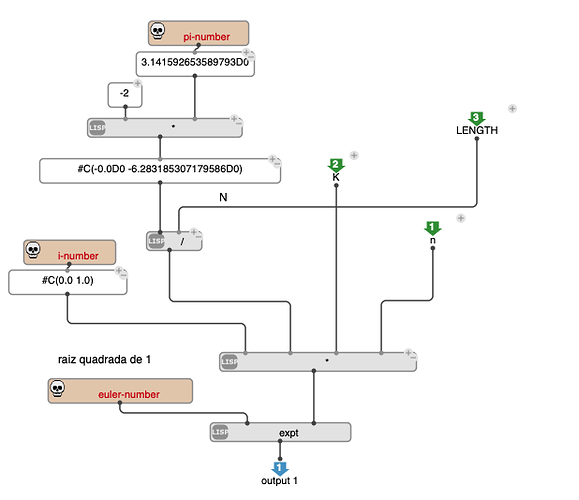
Apparently, I already did. Here is Mathematica’s result for the DFT of {1,0,0,0,1,0,0,1,0,0,0,0,0,0,0,0} (16 elements):
{3. + 0. I, 0.0761205 - 1.38268 I, 0.707107 + 0.707107 I, 0.617317 + 0.0761205 I, 2. + 1. I, 1.38268 - 1.92388 I, -0.707107 + 0.707107 I, 1.92388 + 0.617317 I, 1. + 0. I, 1.92388 - 0.617317 I, -0.707107 - 0.707107 I, 1.38268 + 1.92388 I, 2. - 1. I, 0.617317 - 0.0761205 I, 0.707107 - 0.707107 I, 0.0761205 + 1.38268 I}
You can test it directly with bach.fft’s own tutorial (and yeah, it’s called FFT but it actually computes the DFT as they explain it themselves.)
Your own OM FFT patch gives the same result as Mathematica and bach, but for some reason your OM# DFT patch doesn’t. I can’t see any mistakes in your patch, but it’s definitely going wrong somewhere.
It seems to be some weird problem with this patch implementation, with the lisp code I have a very close result.
#C(2.999999999999999D0 -5.551115123125783D-17)
#C(-0.3660254037844366D0 -0.3660254037844385D0)
#C(0.9999999999999996D0 2.220446049250313D-16)
#C(1.9999999999999974D0 0.9999999999999993D0)
#C(2.4424906541753444D-15 -1.7320508075688763D0)
#C(1.366025403784435D0 1.366025403784438D0)
#C(1.0D0 -3.5426305985963857D-16)
#C(1.3660254037844389D0 -1.366025403784436D0)
#C(-4.218847493575595D-15 1.732050807568874D0)
#C(2.000000000000001D0 -0.9999999999999977D0)
#C(0.9999999999999987D0 5.551115123125783D-16)
#C(-0.3660254037844388D0 0.3660254037844338D0))
If I run it using Python Numpy FFT have same as you:
(#C(3.0 -0.0)
#C(-0.36602542 -0.36602542)
#C(1.0 0.0)
#C(2.0 1.0)
#C(0.0 -1.7320508)
#C(1.3660255 1.3660255)
#C(1.0 -0.0)
#C(1.3660255 -1.3660255)
#C(0.0 1.7320508)
#C(2.0 -1.0)
#C(1.0 -0.0)
#C(-0.36602542 0.36602542)
I’ll see what’s going on with the patch.
Let me know if you find something!
Now is fixed, When you asked for the DFT patch I did some quick modifications because it was configured to work just with DFT-Size 4096, because that, I forgot to add the 1+ to calculate the N. N was being calculated N - 1 (because of the index).
Sorry!
DFT-fixed.opat (31.5 KB)
Hi Charles,
Thank you so much for the patch, it’s flawless. I’ve ported it to OM and added a simple pc-set converter:
dft.omp (27.1 KB)
All the best,
António
